In der numerischen Strömungsmechanik (CFD) gibt es mehr als eine Möglichkeit zu beschreiben, wie sich Fluide bewegen, vermischen und mit ihrer Umgebung interagieren. Seit Jahrzehnten dient die Finite-Volumen-Methode (FVM) als Standard und bildet das Rückgrat der meisten kommerziellen und akademischen CFD-Löser. Da Anwendungen jedoch komplexer werden und heftiges Schwappen, freie Oberflächen oder bewegliche Bauteile beinhalten, haben sich partikelbasierte CFD-Methoden als überzeugende Alternative herauskristallisiert.
Beide Ansätze lösen die gleichen physikalischen Grundgleichungen, d. h. die Navier-Stokes-Gleichungen. Dennoch ist die Art und Weise, wie sie Fluide darstellen, Wechselwirkungen berechnen und Geometrie handhaben, grundlegend unterschiedlich. Das Verständnis dieser Unterschiede hilft Ingenieuren, das richtige numerische Werkzeug für die Physik zu wählen, die sie erfassen möchten.
Von Gittern zu Partikeln – Ein Perspektivwechsel
Die FVM nähert sich der Fluidbewegung aus einer eulerschen Perspektive. Sie unterteilt das Simulationsgebiet in ein Gitter von Kontrollvolumina und berechnet den Fluss von Masse, Impuls und Energie zwischen ihnen. Im Gegensatz dazu verfolgt die partikelbasierte CFD einen Lagrange-Ansatz und konzentriert sich auf die direkte Bewegung und Wechselwirkungen diskreter Fluidpakete.
Bei FVM bewegt sich das Fluid durch ein festes oder bewegliches Gitter, während bei Partikel-CFD das Gitter fehlt und eine dynamische Wolke interagierender Partikel das Fluid repräsentiert. Obwohl der Unterschied subtil erscheinen mag, hat er erhebliche Auswirkungen auf numerische Stabilität, Flexibilität und Skalierbarkeit.
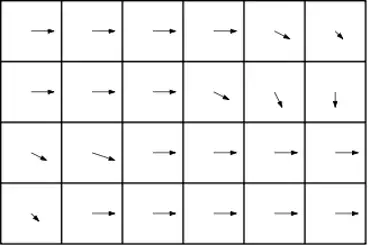
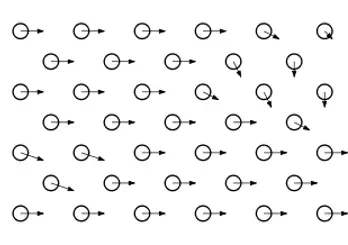
Die Finite-Volumen-Methode
FVM ist eine grundlegende Technik in der CFD, weil sie die Prinzipien der Erhaltung von Masse, Impuls und Energie wahrt. Sie stellt sicher, dass die Menge an Materie, die in ein Kontrollvolumen eintritt, der Menge entspricht, die das Kontrollvolumen verlässt. Durch Integration der Erhaltungsgleichungen über jede Zelle und Anwendung des Divergenztheorems wandelt FVM Differentialgleichungen in algebraische Formen um, die Löser effizient handhaben können. Dieses Framework garantiert globale Erhaltung, selbst beim Umgang mit komplexen, unstrukturierten Gittern.
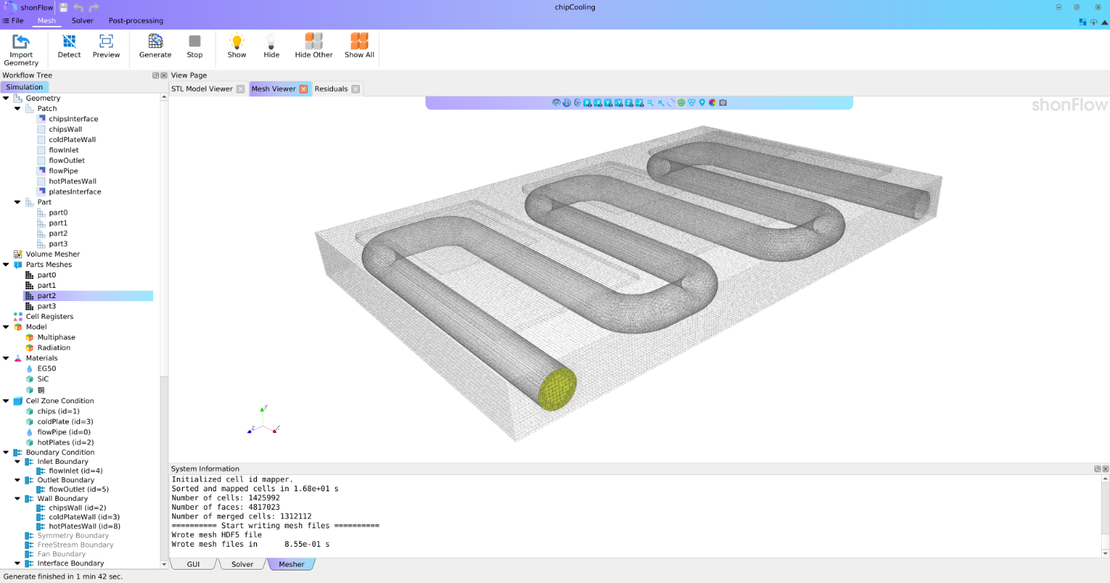
Die Vorteile von FVM sind weithin anerkannt:
- Hohe numerische Genauigkeit und strikte Erhaltung von Flüssen.
- Eine breite Palette von Turbulenz- und Verbrennungsmodellen, die über Jahrzehnte validiert wurden.
- Robuste Handhabung von Randbedingungen für Wände, Einlässe und Auslässe.
- Starke Skalierbarkeit auf parallelen Rechnerarchitekturen.
Diese Eigenschaften machen FVM besonders geeignet für Anwendungen, bei denen die Domänengeometrie fest ist und die Strömung kontinuierlich bleibt, wie in der Aerodynamik, Turbomaschinen oder Elektronikkühlung. Die Abhängigkeit von FVM von der Gitterqualität stellt jedoch Herausforderungen dar. Wenn sich Geometrien verformen oder Grenzflächen auseinanderbrechen, wie bei Spritzen, Fragmentierung oder Strömungen mit freien Oberflächen, wird die Aufrechterhaltung der Gitterqualität zunehmend komplex.
Der partikelbasierte Ansatz
Partikel-CFD hingegen verzichtet vollständig auf das Gitter. Jedes Partikel repräsentiert eine kleine Masse Fluid und trägt seine eigene Geschwindigkeit, seinen Druck und seine thermodynamischen Eigenschaften. Diese Partikel interagieren durch Kernfunktionen, die ihre lokale Nachbarschaft definieren.
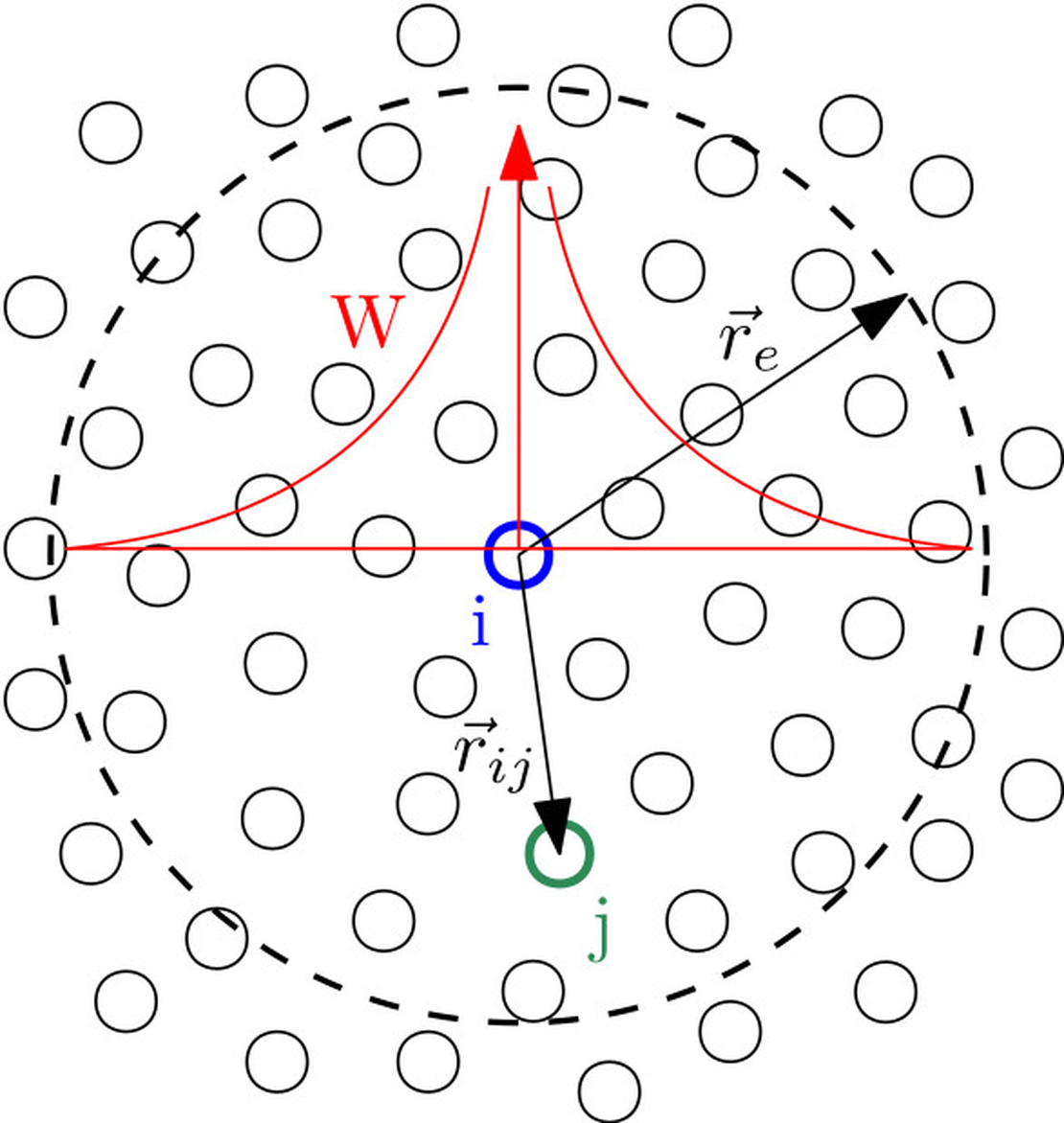
Die Bedeutung des Einflusses eines benachbarten Partikels auf ein anderes kann hier durch eine einfache Gewichtsfunktion berechnet werden:
Beliebte Varianten der Lagrange-basierten Partikel-CFD sind die Smoothed-Particle-Hydrodynamics-Methode (SPH) oder die Moving-Particle-Semi-Implicit-Methode (MPS). Da die Methode vollständig Lagrange-basiert ist, folgt die Bewegung der Partikel natürlich der Strömung. Es gibt kein Gitter, das sich verformt, keine Notwendigkeit für Neuvernetzung und keine topologischen Einschränkungen.

Dies macht Partikel-CFD besonders leistungsfähig für:
- Strömungen mit freien Oberflächen und Schwappen (z. B. flüssige Kraftstofftanks, Wellen-Struktur-Wechselwirkungen).
- Fluid-Struktur-Interaktion (FSI), bei der sich feste Ränder bewegen oder verformen.
- Mehrphasen- und Granulatsysteme, wie Suspensionen oder Pulverströmungen.
- Phasenwechselprozesse, wie Schmelzen, Erstarrung oder Spraydynamik.
Seine gitterfreie Natur macht die Vorverarbeitung weitaus einfacher, das Geometrie-Setup wird schneller, insbesondere für komplexe oder sich entwickelnde Domänen.
Wahl des richtigen Ansatzes
Die Wahl zwischen Partikel-CFD und Finite-Volumen-CFD wird mehr durch die Physik des Problems bestimmt als durch persönliche Präferenzen:
- Für stationäre Strömungen, Strömungen mit hoher Reynolds-Zahl oder thermische Strömungen ist die FVM unübertroffen.
- Für hochgradig transiente, mehrphasige oder verformende Systeme erfasst Partikel-CFD effektiv Komplexitäten, die traditionelle Gitter nicht bewältigen können.
Erfahrene Simulationsingenieure betrachten diese beiden Methoden zunehmend als komplementär; sie sind wie verschiedene Instrumente im selben numerischen Orchester, jedes für einen einzigartigen Aspekt der Fluidbewegung geeignet.
CFD über traditionelle Grenzen hinaus vorantreiben
Wir sehen derzeit, wie sich sowohl Partikel-CFD als auch FVM an neue Rechnerarchitekturen anpassen. Dies ermöglicht noch größere und detailliertere Simulationen für beide Ansätze. Fortschritte bei beweglichen und anpassbaren Gittern im Bereich der FVM und variablen Partikelgrößen in der Lagrange-CFD verschieben die Grenzen des Möglichen noch weiter und zeigen gewissermaßen eine Konvergenz der Methoden in ihren Anwendungsfeldern am Horizont.
Letztendlich zielen sowohl Finite-Volumen- als auch Partikelmethoden darauf ab, Ingenieuren zu helfen, das Unsichtbare zu visualisieren, insbesondere das Verhalten von Fluiden vorherzusagen, die unsere Umwelt prägen.

