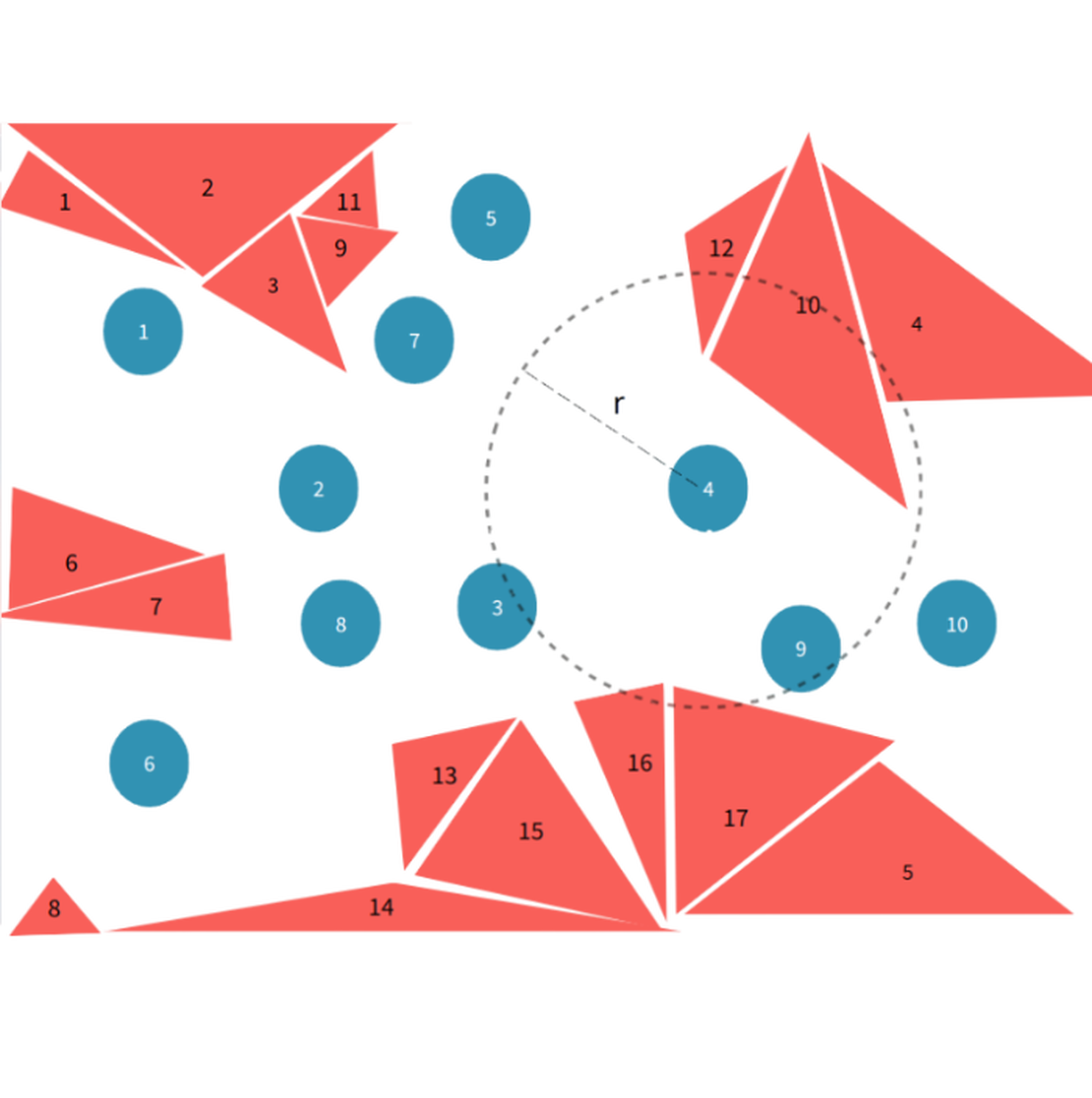
Die Partikelmethode diskretisiert Flüssigkeiten oder Feststoffe in diskrete Recheneinheiten, bekannt als Partikel. Bei Feststoffen werden geometrische Informationen durch dreieckige Oberflächenelemente unterschiedlicher Größen dargestellt. Jedes Oberflächenelement, das mit einem Partikel interagiert, wird in ein Geisterwandpartikel umgewandelt, wodurch sichergestellt wird, dass sowohl feste Grenzen als auch Fluidbereiche einheitlich in Partikelform dargestellt werden. Diese einheitliche Darstellung ermöglicht es, dass sich numerische Berechnungen ausschließlich auf Partikel-Partikel-Interaktionen konzentrieren.
Bei der Partikelmethode interagiert jedes Partikel mit seiner Umgebung innerhalb eines endlichen Einflussradius . Eine Kugel mit Radius , zentriert am Partikel, definiert den Einflussbereich. Alle Partikel, die sich innerhalb dieser Kugel befinden, werden als Nachbarpartikel bezeichnet, und alle dreieckigen Flächen innerhalb dieser Kugel werden als benachbarte Dreiecksflächen identifiziert.
Problembeschreibung
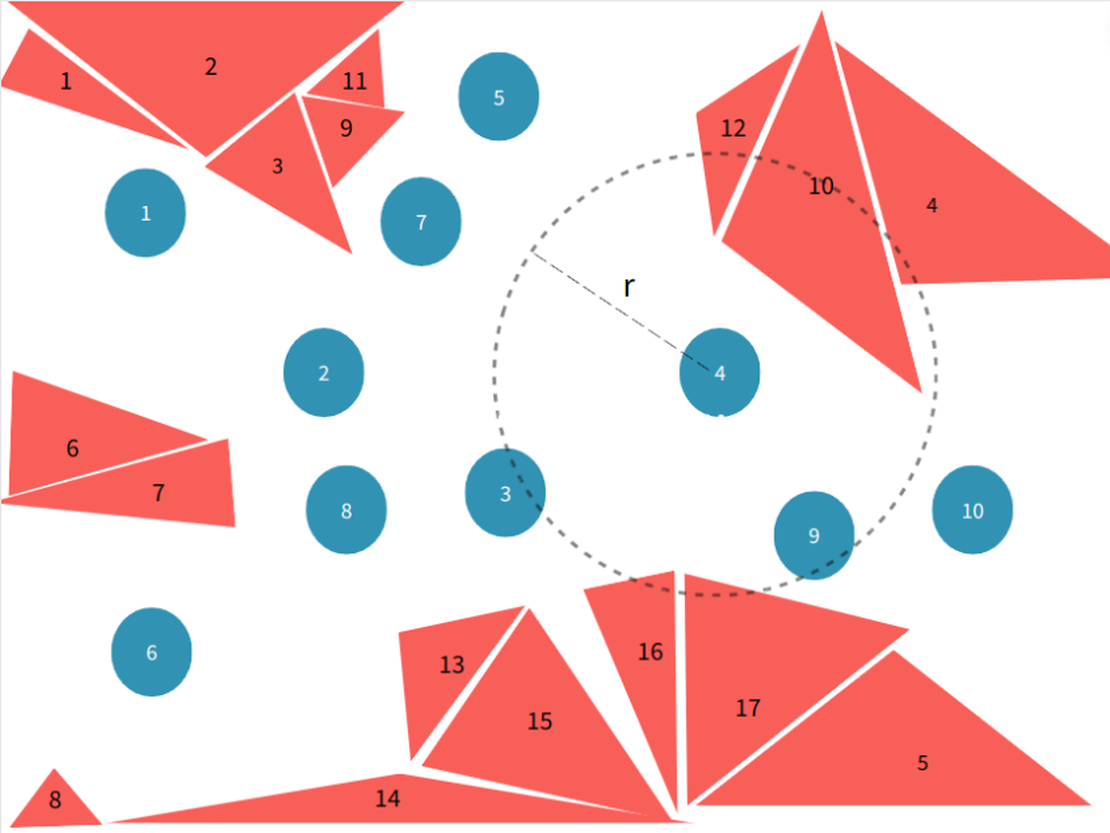
Eine bestimmte Anzahl von Partikeln und Dreiecksflächen sind zufällig im dreidimensionalen Raum verteilt. Die Interaktion zwischen Partikeln und Flächen hat einen Einflussbereich . Eine Kugel mit Radius , zentriert an einem gegebenen Partikel, wird definiert, und die Dreiecksflächen innerhalb dieser Kugel werden als benachbarte Dreiecksflächen dieses Partikels bezeichnet. Die Aufgabe besteht darin, alle benachbarten Dreiecksflächen für jedes Partikel zu identifizieren.
Implementierungsansatz
Durch das Zeichnen eines Gitters im 3D-Raum wird jede dreieckige Oberfläche in der Umgebung darauf abgebildet. Ein oder mehrere Gitterelemente segmentieren jede dreieckige Oberfläche und transformieren die Positionsbeziehung zwischen Partikeln und Oberflächen in eine Beziehung zwischen Gitterelementen.
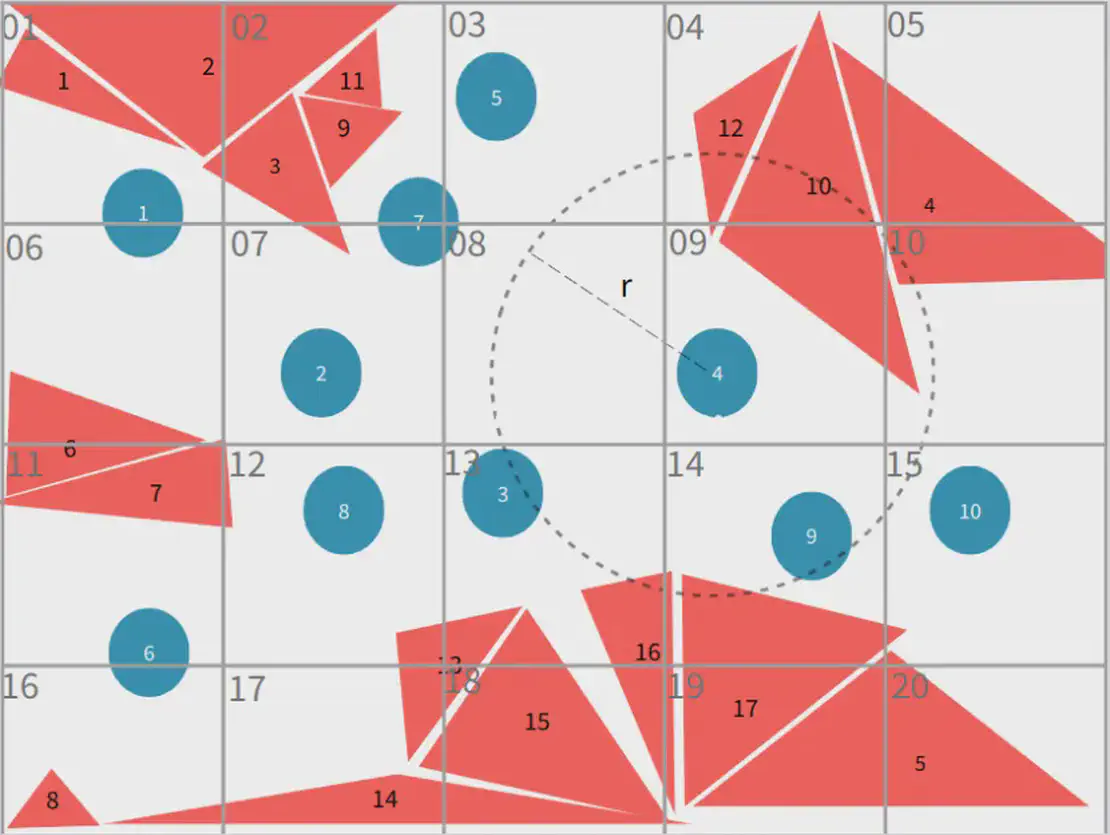
Die Kantenlänge der Gitterzelle wird gleich dem Einflussradius des Partikels gewählt. Bei der Bestimmung der benachbarten Flächen für ein Partikel genügt es, Flächen innerhalb der eigenen Gitterzelle des Partikels und der 26 umgebenden benachbarten Zellen im 3D-Raum zu untersuchen. Durch Vergleich der tatsächlichen Abstände zwischen dem Partikel und diesen Dreiecksflächen mit dem Einflussradius r können alle gültigen benachbarten Dreiecksflächen effizient identifiziert werden.
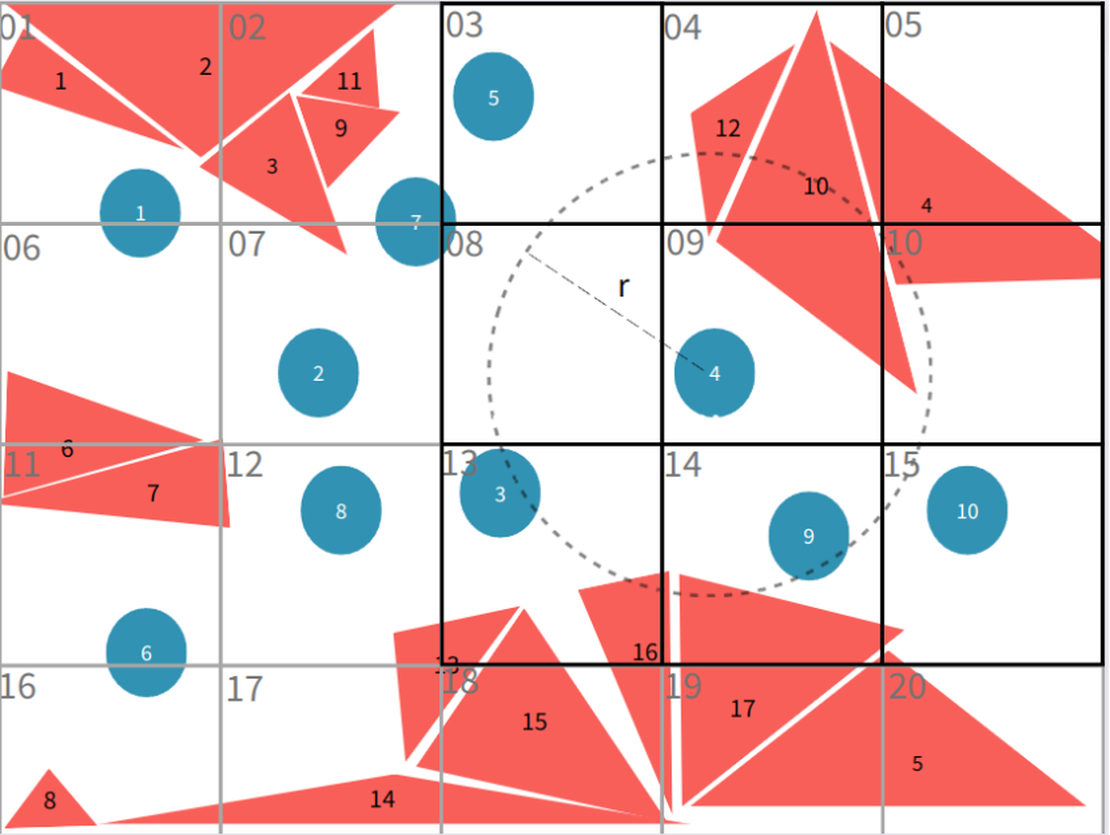
Im zweidimensionalen Szenario muss die Suche bei der Lokalisierung der benachbarten Dreiecksflächen von Partikel 4 nur Flächen (4, 5, 10, 12, 13, 15, 16, 17) berücksichtigen, die sich in Gitter 9 und seinen angrenzenden Gittern (3, 4, 5, 8, 9, 10, 13, 14, 15) befinden. Diese lokalisierte Suche reduziert die Rechendomäne drastisch und senkt die Zeitkomplexität.
Parallele Suche
Dieser Algorithmus verwendet einen hybriden Parallelansatz, der Datenparallelität und Aufgabenparallelität kombiniert. Alle Partikeldaten sind auf mehrere MPI-Prozesse verteilt, wobei jeder Prozess vollständige Festkörperdaten enthält. Die Gitterinformationen werden parallel durchlaufen, wobei Abstände zwischen Partikeln und Flächen in benachbarten Gittern berechnet werden.
Da jede Operation unabhängig ist und keine Kommunikation beinhaltet, ist sie ein erstklassiger Kandidat für parallele Verarbeitung.
Optimierungspunkte
Eine einfache Gittersuche nach Dreiecks-IDs innerhalb benachbarter Gitter kann doppelte IDs ergeben. Beispielsweise könnte Flächen-ID 10 in den Gittern 4, 9 und 10 erscheinen, wenn Partikel 4 nach Nachbarn sucht – was zu redundanten Berechnungen führt. Daher muss eine Duplikatfilterung implementiert werden, um sicherzustellen, dass jede Dreiecksfläche nur einmal pro Partikel berücksichtigt wird.
Erweiterungen
Speicherung von Festkörperinformationen
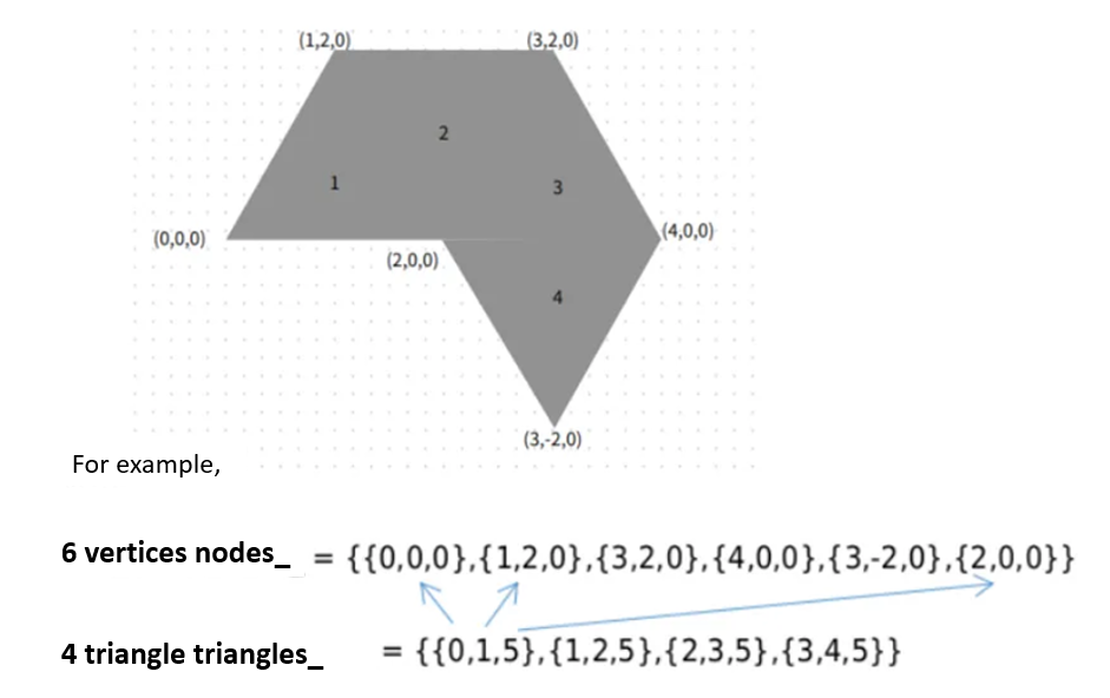
- nodes: Scheitelpunktkoordinaten aller Dreiecksflächen.
- triangles: Scheitelpunktkonnektivität jeder Fläche.
Gitterinformationen (zValue)
Dieser Algorithmus verwendet die Hilbert-Kurve, um dreidimensionale Gitterkoordinaten in eindimensionale Identifikatoren abzubilden. Die dreidimensionalen Gitterdaten (x, y, z) werden über die Hilbert-Kurve auf eine eindimensionale Darstellung reduziert. Jeder Gitterpunkt (x, y, z) wird als Long-Integer (zValue) aufgezeichnet. Die Morton-Kodierung wandelt die Gitterkoordinaten (x, y, z) in einen Long-Integer (zValue) um, und umgekehrt können die Gitterinformationen (x, y, z) aus zValue über die Morton-Kodierung abgerufen werden.